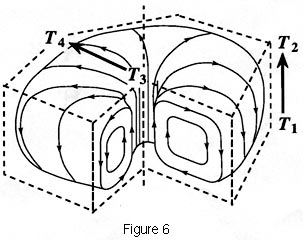
The autocatakinetic flow constituting a Bénard cell is shown by the small arrows. T1-ðT2 is the heat gradient between the source and sink that motivates the flow. As heat rises through the center it creates a surface tension gradient T3-ðT4 which acts to further amplify the upward flow by pulling the hotter fluid to the cooler surrounds where it falls to the bottom to be heated again. (From Swenson, 1997a. Copyright 1977 JAI Press. Used by permission).

Beyond making the epistemic dimension of the world entirely anomalous and incommensurable with the physical part, however, the Boltzmann view is readily falsified by simple physical experiments, such as the Bénard experiment shown above (Figures 5 and 6), where dynamic order is seen to arise not infinitely improbably, but with a probability of one, that is, every time and as soon as it gets the chance (Swenson & Turvey, 1991). Rather than incommensurabilty, this suggests a universality to spontaneous ordering implying a unification the two "rivers" and a principled or nomological basis for ecological relations.

Bertalanffy, Schroedinger, and Prigogine: Autocatakinetics and the Balance Equation of the Second Law

As the preceding indicates dynamically ordered systems are members of a class of systems which includes both living and non-living members. In particular, individual living things, human cultural systems, and the planetary system as a whole (e.g., see Swenson & Turvey, 1991) as well as non-living systems such as Benard cells, tornadoes, and dust devils-systems constituted by dynamic order-are all "autocatakinetic" systems. Autocatakinetic systems are systems whoseidentities are constituted with a set of circularly causal relations through the continuous flux of their components in the breakdown or dissipation of environmental or field potentials (Swenson, 1991a, Swenson & Turvey, 1991). Persistence (the form of the thing) at the "macro" level is constituted by change at the "micro" level through the flux pulled in across the system's boundaries and

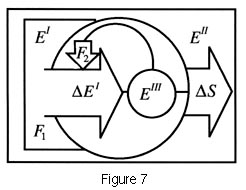
A generalized autocatakinetic system. EI and EII indicate a source and a sink with the difference between them constituting a field potential with a thermodynamic force F1 (a gradient of a potential) the magnitude of which is a measure of the difference between them. is the energy flow at the input, the drain on the potential which is transformed into entropy production at the output. EIII is the internal potential carried in the circular relations that define the system by virtue of its distance from equilibrium that acts back to amplify or maintain input during growth or non-growth phases respectively with an internal force F2. (From Swenson, 1989b. Copyright 1989 by Pergamon. Adapted by permission).

expelled in a more degraded form into the environment. Figure 7 shows a schematic of an autocatakinetic system. The reader will notice that this is a more explicit representation of the conjunction presented as the minimal ontology above (Figure 1). With this figure, and with the discussion of the conservation of the first law and the one-way flow of the second law in the previous section, we take significant further steps towards the explicit a posteriori recovery of the a priori given, a task to be completed, in general form, with additional steps below.
The first and second laws provide a principled basis for their respective entailments, but the whole class of autocatakinetic systems, and active opportunistic ordering by which they are constituted from the widely received view of the second law still goes against universal law. An important contribution was made towards this discourse in the middle of this century by Bertalanffy (1952) who showed that "spontaneous order...can appear" in systems with energy flowing through them, and Schroedinger (1945), who, comparing living things to flames, pointed out that such systems (all autocatakinetic systems) do not violate the second law as long as they produce entropy (or minimize potentials) at sufficient rates to compensate for their ordering (their increase in space-time dimensions or internal entropy reduction) and thereby satisfy the balance equation of the second law. The idea was further popularized by Prigogine (1978) under the name of "dissipative structures". Whereas such systems were thus given "permission" to exist given the classical view of the second law, according to Boltzmann's interpretation, however, they were still 'infinitely improbable'. The question of why order is seen to arise whenever it gets the chance, in simple physical systems, in the evolutionary record writ large (e.g., see Swenson & Turvey, 1991), in the "fecundity principle" on which Darwinian theory depends, and in the directedness towards that characterizes the intentional content of the epistemic act itself remained.