The second law was formulated in the middle of the last century by Clausius and Thomson following Carnot's earlier observation that, like the fall or flow of a stream that turns a mill wheel, it is the "fall" or flow of heat from higher to lower temperatures that motivates a steam engine. The key insight was that the world is inherently active, and that whenever an energy distribution is out of equilibrium a potential or thermodynamic "force" (the gradient of a potential) exists that the world acts spontaneously to dissipate or minimize. All real-world change or dynamics is seen to follow, or be motivated, by this law. So whereas the first law expresses that which remains the same, or is time-symmetric, in all real-world processes the second law expresses that which changes and motivates the change, the fundamental time-asymmetry, in all real-world process. Clausius coined the term "entropy" to refer to the dissipated potential and the second law, in its most general form, states that the world acts spontaneously to minimize potentials (or equivalently maximize entropy), and with this, active end-directedness or time-asymmetry was, for the first time, given a universal physical basis. The balance equation of the second law, expressed as S > 0, says that in all natural processes the entropy of the world always increases, and thus whereas with the first law there is no time, and the past, present, and future are indistinguishable, the second law, with its one-way flow, introduces the basis for telling the difference.
The active nature of the second law is intuitively easy to grasp and empirically demonstrate. If a glass of hot liquid, for example, as shown in Figure 3, is placed in a colder room a potential exists and a flow of heat is spontaneously produced from the cup to the room until it is minimized (or the entropy is maximized) at which point the temperatures are the same and all flows stop.

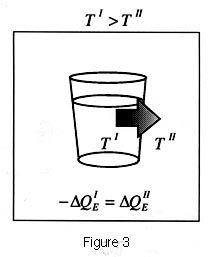
A glass of liquid at temperature TI is placed in a room at temperature TII such that . The disequilibrium produces a field potential that results in a flow of energy in the form of heat from the glass to the room so as to drain the potential until it is minimized (the entropy is maximized) at which time thermodynamic equilibrium is reached and all flows stop. refers to the conservation of energy in that the flow from the glass equals the flow of heat into the room. (From Swenson, 1991a. Copyright 1991 Intersystems Publications. Adapted by permission).

Figure 4 shows various other potentials and the flows they would produce. Of important theoretical interest for this paper is the fact that Joule's experiment (Figure 2) while designed to

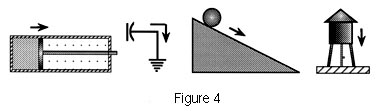
Further examples of potentials that follow from nonequilibrium distributions of energy. Whenever energy (in whatever form) is out of equilibrium with its surroundings, a potential exists for producing change that, following the second law, is spontaneously minimized.

show the first law unintentionally demonstrates the second too. As soon as the constraint is removed the potential produces a flow from the falling weight through the moving paddle through the thermometer. This is precisely the one-way action of the second law and the experiment depends upon it entirely. The measurement of energy only takes place through the lawful flow or time-asymmetry of the second law, and the point to underscore is that the same is true of every measurement process. In addition, every measurement process also a demonstrates the first law as well since the nomological relations that hold require something that remains invariant over those relations (or else one could not get invariant or nomological results). The first and second laws are thus automatically given in every measurement process for the simple fact, in accordance with the discussion above, that they are entailed in every epistemic act (Swenson, in press a, b; see also Matsuno, 1989, in press on generalized measurement). Here we begin to make the appropriate steps towards the a posteriori recovery of the a priori given. It is just this reconciliation that sets the tolerance space with respect to uniting the otherwise incommensurable rivers and providing a principled account of the epistemic dimension and the constitutive ecological relations that instantiate it.

Boltzmann's View of the Second Law as a Law of Disorder: A Fatal Problem for Ecological Relations

The active macroscopic nature of the second law posed a direct challenge to the "dead" mechanical world view which Boltzmann tried to meet in the latter part of the last century by reducing the second law to a law of probability following from the random collisions of mechanical particles (efficient cause (see Swenson (1990)). Following the lead of Maxwell who had modeled gas molecules as colliding billiard balls, Boltzmann argued that the second law was simply a consequence of the fact that since with each collision nonequilibrium distributions would become increasingly disordered leading to a final state of macroscopic uniformity and microscopic disorder. Because there are so many more possible disordered states than ordered ones, he concluded, a system will almost always be found either in the state of maximum disorder or moving towards it.
As a consequence, a dynamically ordered state, one with molecules moving "at the same speed and in the same direction," Boltzmann (1974/1886, p. 20) asserted, is thus "the most improbable case conceivable...an infinitely improbable configuration of energy." Because this idea works for certain near equilibrium systems such as gases in boxes, and because science until recently was dominated by near equilibrium thinking, Boltzmann's attempted reduction of the second law to a law of disorder became widely accepted as the second law rather than simply an hypothesis about the second law, and one that we now know fails. It became the apparent justification from physics for solidifying Cartesian incommensurability and establishing the view of the two incommensurable rivers-the "river" of biology, psychology, and culture, or the epistemic dimension of the world characterized by intentional dynamics and flowing up to increasingly higher states of order, versus the "river" of physics flowing down to disorder. Such a view is entirely inimical to a science of ecological relations, since, as noted above, it is precisely through the interface of these two rivers that these relations occur, and if the interface is incommensurable then the relations are effectively prohibited, or at best, incomprehensible.

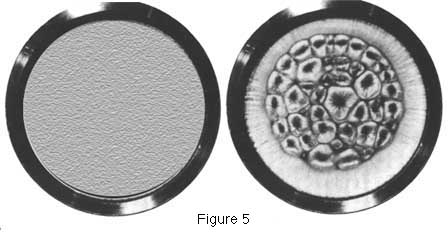
Two time slices from the Bénard experiment. When the gradient of the potential (the "force") between source (the heated surface below) and the sink (the cooler air at the top) is below a critical threshold (left) the flow of heat is produced by the random collision of the molecules (conduction), and the system is in the disordered or "Boltzmann regime", and the surface of the system is smooth, homogeneous, and symmetrical. When the force is above the critical threshold (right), however, the symmetry of the system is broken and autocatakinetic order spontaneously arises as random microscopic fluctuations are amplified to macroscopic levels and "Benard cells" fill the container as hundreds of millions of molecules begin moving together (for more detailed discussion see e.g., Swenson, 1989a,b, c, 1992, 1997a). (From Swenson, 1989c. Copyright 1989 Pergamon Press. Used by permission).