The Law of Maximum Entropy Production or Why the World is in the Order Production Business

The solution to the puzzle is found in two parts. The first is the recognition of an important point found implicitly in the Bertalanffy-Schroedinger-Prigogine contribution not pointed out explicitly by them. In particular, since to come into being and persist an autocatakinetic system must increase the rate of entropy production of the system plus environment at a sufficient

The discontinuous increase in the rate of heat transport that follows from the disorder-to order transition in a simple fluid experiment similar to that shown in Figure 4. The rate of heat transport in the disordered regime is given by, and is the heat transport in the ordered regime [3.1 x 10-4H(cal x cm.-2 x sec-1)]. (From Swenson, 1989a. Copyright 1989 IEEE. Reprinted by permission).

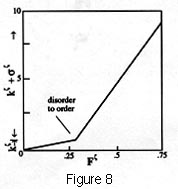
rate to satisfy the balance equation of the second law, ordered flow, according to the balance equation, must be more efficient at dissipating potentials that disordered flow (Swenson, 1989d, 1997a, b; Swenson & Turvey, 1991). Figure 8 shows the dramatic increase in the rate at which the potential is minimized, for example, in the Benard cell experiment in the transition from the disordered to ordered regime, and the balance equation tells us that this is precisely what must happen.
Now this becomes important only with the second part of the solution which is the answer to a question that did not arise in the Bertalanffy-Schroedinger-Prigogine discourse, nor was it a question that classical thermodynamics ever asked. In particular, it is which path(s) out of available paths will a system take to minimize potentials or maximize the entropy? The answer (the "law of maximum entropy production") is the path or assembly of paths that minimizes the potential (maximizes the entropy) at the fastest rate given the constraints (Swenson, 1988, 1989d, 1991a,b, 1997a,b; Swenson & Turvey, 1991), and like the second law, the law of maximum entropy production is intuitively easy to grasp and empirically demonstrate. Imagine any out of equilibrium system with multiple available pathways such as a heated cabin in the middle of snowy woods (Swenson & Turvey, 1991). In this case, the system will produce flows through the walls, the cracks under the windows and the door, and so on, so as to minimize the potential. What we all know intuitively (why we keep doors and windows closed in winter) is that whenever a constraint is removed so as to provide an opportunity for increased flow the system will reconfigure itself so as to allocate more flow to that pathway leaving what it cannot accommodate to the less efficient or slower pathways. In short, no matter how the system is arranged the pattern of flow produced will be the one that minimizes the potential at the fastest rate given the constraints. Once the idea is grasped, examples are easy to proliferate (e.g., see also Dyke, 1997; Goerner, 1994; Peck, in press).
What does the law of maximum entropy production have to do with order production? Given the foregoing, the reader may have already jumped to the correct conclusion, namely, if ordered flow produces entropy faster than disordered flow (as required by the balance equation of the second law), and if the world acts to minimize potentials at the fastest rate given the constraints (the law of maximum entropy production), then the world can be expected to produce order whenever it gets the chance (Swenson, 1989d, 1991a, b, 1997a, b; Swenson & Turvey, 1991). The world can be expected to act opportunistically in the production of dynamical order because potentials are thereby minimized at a faster rate. The world, in short, is in the order production business because ordered flow produces entropy faster than disordered flow, and this, in most direct terms, provides the nomological basis for the reconciliation of the otherwise two incommensurable rivers. Rather than being anomalous with respect to, or somehow violating physical law, the "river that flows uphill" that characterizes the active epistemic dimension of the world is seen to be a direct manifestation of it. The constitutive logic of ecological relations as expressed in autocatakinesis and the minimal ontology is seen as a direct consequence of universal law.

The Nomological Basis for Semantic Content

A mostly implicit point so far that bears brief elaboration is the relationship between order production and the development or extension of space-time. In particular, the spontaneous production of order constitutes a dramatic increase in space-time dimensions. This is well demonstrated, again, by the Bénard experiment (see Figures 5) where in the disordered regime the intrinsic space-time dimensions are defined by mean free paths distances and relaxation times (the distances and times between random or disordered collisions) on the order of 10-8 centimeters and 10-15 seconds, while in the ordered regime, in contrast, the intrinsic space-time dimensions are of the order of seconds and centimeters. It takes the fluid some seconds to make the autocatakinetic cycle that constitutes each cell and the distances is measured in centimeters (see Figure 6). Significantly, these new space-time dimensions do not exist in the disordered regime. They literally come into being with the production of order, and this understanding takes us to the main point of this section.
In particular, if we understand from universal principles that the world acts, in effect, to maximize its extension into space-time, to produce as much order as possible, we can see immediately what intentional dynamics provide. By providing the means for linking together or accessing and dissipating, discontinuously located, or non-local, potentials in the building of order, intentional dynamics provides access to vast otherwise inaccessible regions of space-time, and this is precisely what intentional dynamics, or ecological relations do. The autocatakinesis of non-living systems such as Bénard cells, tornadoes, or dust devils are maintained, or determined, with respect to local potentials within which they are proximally, and continuously, embedded. If the potentials are removed (e.g., the heat in the Bénard case) they collapse and "die". In contrast, it is the signature of the intentional dynamics of living things, or the ecological relations that characterize them, that they are maintained with respect to non-local, distal, and discontinuous potentials through the use of meaning or "information about". Furthermore, if the autocatakinetic relation that characterizes the intentionality of the epistemic act is a directedness towards the maintenance of invariant or persistent relations with distal potentials then there must be a lawful basis for semantic content in the world for meaningful specification in the proximal present of intentional ends in the distal future.
The basis for this was first well appreciated by Gibson (1986/1979; Swenson & Turvey, 1991; Turvey & Shaw, 1995) with his ecological conception of information. Living things are macroscopic systems that maintain their autocatakinesis through the context of macroscopic flow, and what Gibson correctly concluded was that the place to look for meaningful content was not in the normal physical descriptors of individual particles, but instead in the variables of the flow itself. Specifically, what he recognized was that the ambient energy flows (e.g., optical, mechanical, chemical) in which living things are embedded carry invariant macroscopic properties that lawfully specify, and thus carry semantic content with respect to, or 'information about', their sources. This information can then be used directly in the lawful proximal control of behavior towards distal intentional ends.
Optic flow variables, for example, can lawfully specify 'time-to-contact' (e.g., Lee, 1980; Kim et al. 1993; Swenson, 1997a), or a chemical or optical gradient can lawfully specify the source of food (see also Swenson & Turvey, (1991) on the origin of vision), and diffusion and mechanical fields (e.g., see Peck, (in press) on the origin of hearing) can be used in similar ways (e.g., see Lee, 1980; Kim et al. 1993; Swenson, 1997a; Swenson & Turvey, 1991; Turvey & Shaw, 1995). A further elaboration of this point can be made with the case of "time-to-contact", a particularly crucial and widespread requirement for the intentional dynamics characterizing many